Building Layout for Drilling Holes
Reader ROGER in LISBON asks: “What is fastest way to layout a building for drilling holes?” From Hansen Pole Buildings’ Construction Manual:
Building Layout
The building layout establishes exact reference lines and elevations. Care in layout makes construction easier and helps keep building square.
REMINDER: Building width and length are from corner column outside to corner column outside!
After installing all framing, finished framework will normally be 3” wider and longer than ordered or “call out” dimensions. Ignoring this will result in more effort during construction.
Calculating Diagonal Lengths
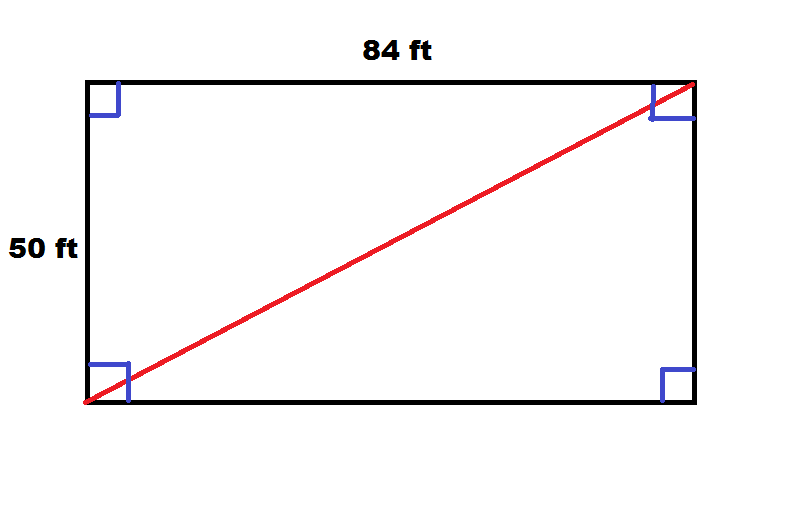
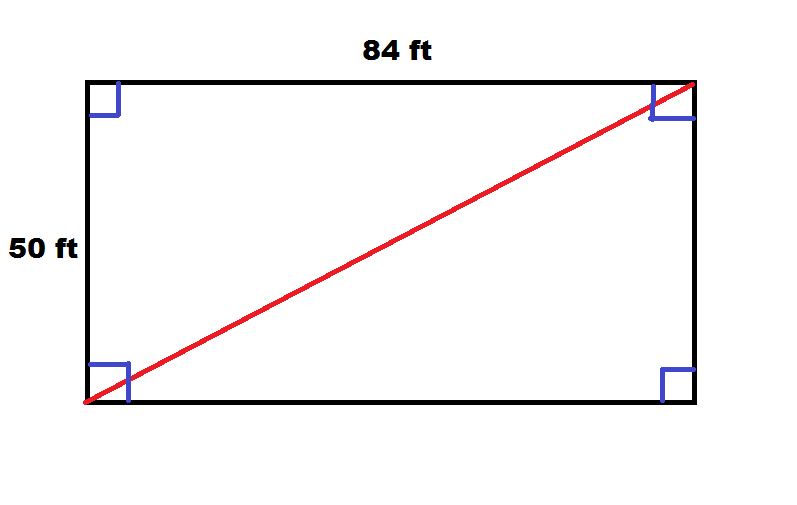
Example: building is 50 feet wide and 84 feet long.
Explanation: A picture helps greatly with this problem, so we begin with a rectangular post frame building.
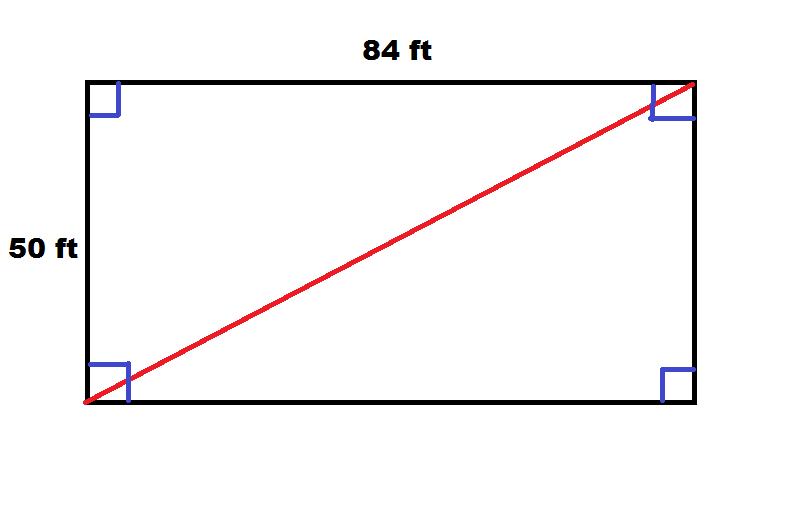
Distance (drawn in red) is diagonal of our rectangle, or k. We should also note this diagonal divides our rectangle into two congruent right triangles. We can therefore find the length of our diagonal by focusing on one of these triangles and determining hypotenuse. This can be done with the Pythagorean Theorem, giving us:
50^2 + 84^2 = k^2
2500 +7056 = k^2
9556 = k^2
Taking square root gives us
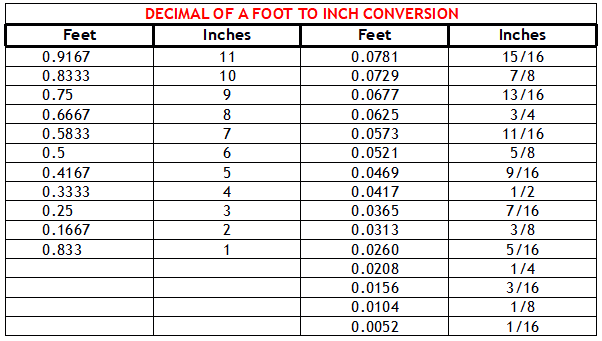
k=97.754795 feet or 97’ 9-1/16”
See Table 4-1 below.
| DECIMAL OF A FOOT TO INCH CONVERSION |
| Feet |
Inches |
Feet |
Inches |
| 0.9167 |
11 |
0.0781 |
15/16 |
| 0.8333 |
10 |
0.0729 |
7/8 |
| 0.75 |
9 |
0.0677 |
13/16 |
| 0.6667 |
8 |
0.0625 |
3/4 |
| 0.5833 |
7 |
0.0573 |
11/16 |
| 0.5 |
6 |
0.0521 |
5/8 |
| 0.4167 |
5 |
0.0469 |
9/16 |
| 0.3333 |
4 |
0.0417 |
1/2 |
| 0.25 |
3 |
0.0365 |
7/16 |
| 0.1667 |
2 |
0.0313 |
3/8 |
| 0.0833 |
1 |
0.0260 |
5/16 |
|
|
0.0208 |
1/4 |
|
|
0.0156 |
3/16 |
|
|
0.0104 |
1/8 |
|
|
0.0052 |
1/16 |
Table 4-1
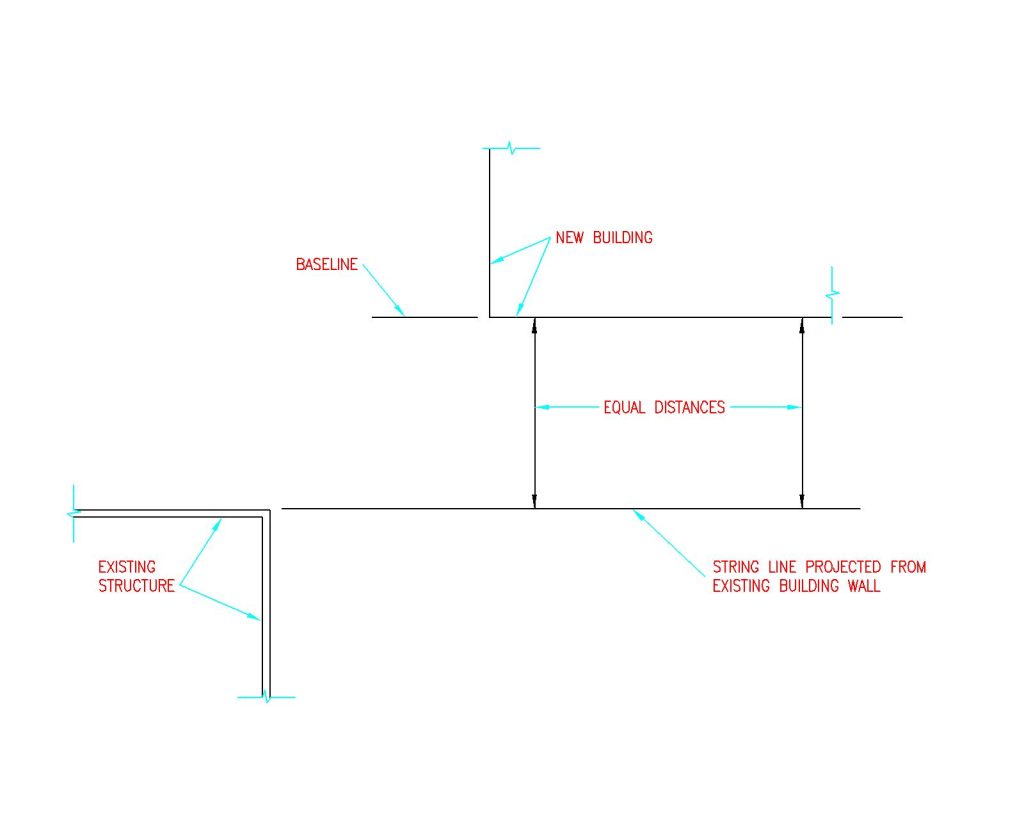
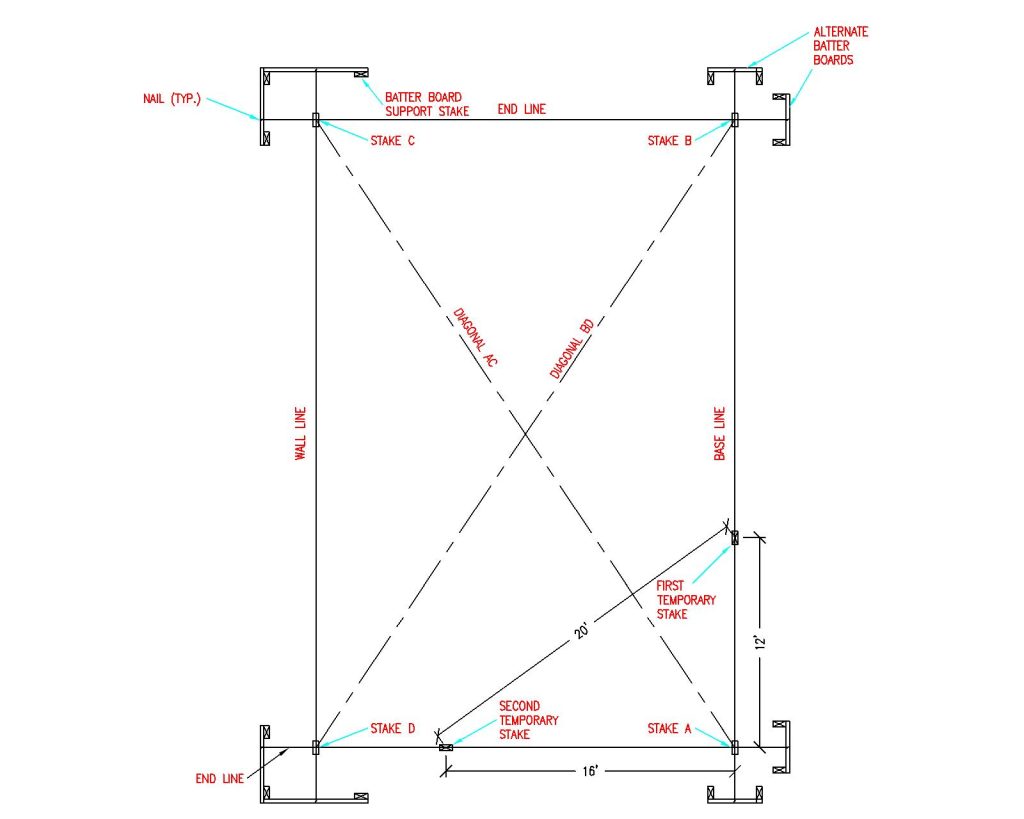
To start, stake out a “base” line string. This will become either building front or side. If trying to align a building with an existing structure, roadway or property lines, have the first wall line parallel to reference point. See Figure 4-1
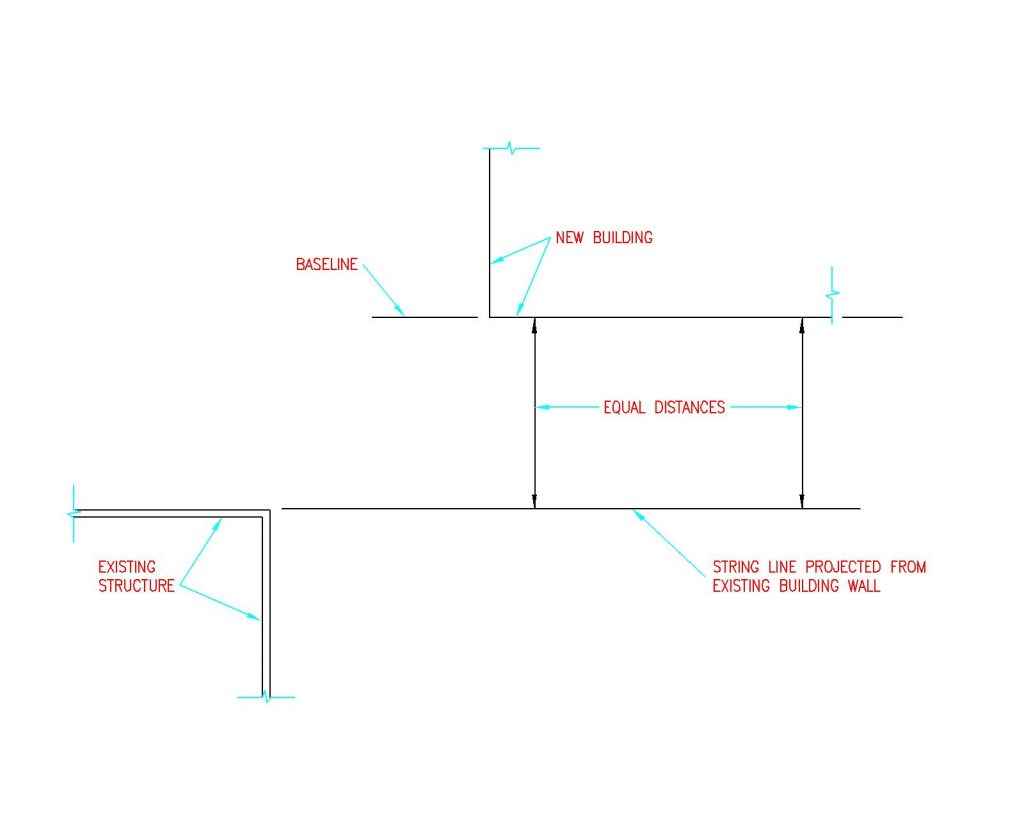
Figure 4-1: Base String Line
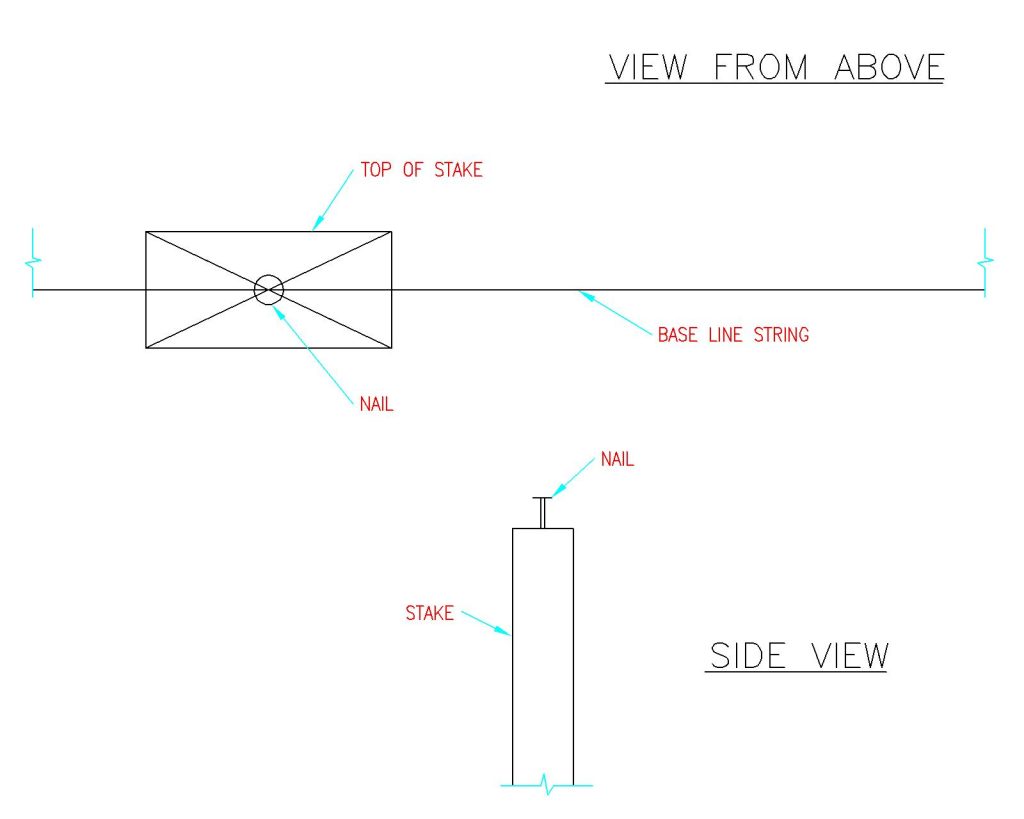
Locate and set front corner stake “A” along the baseline. Drive a nail partially into the stake top as a reference point. See Figure 4-2
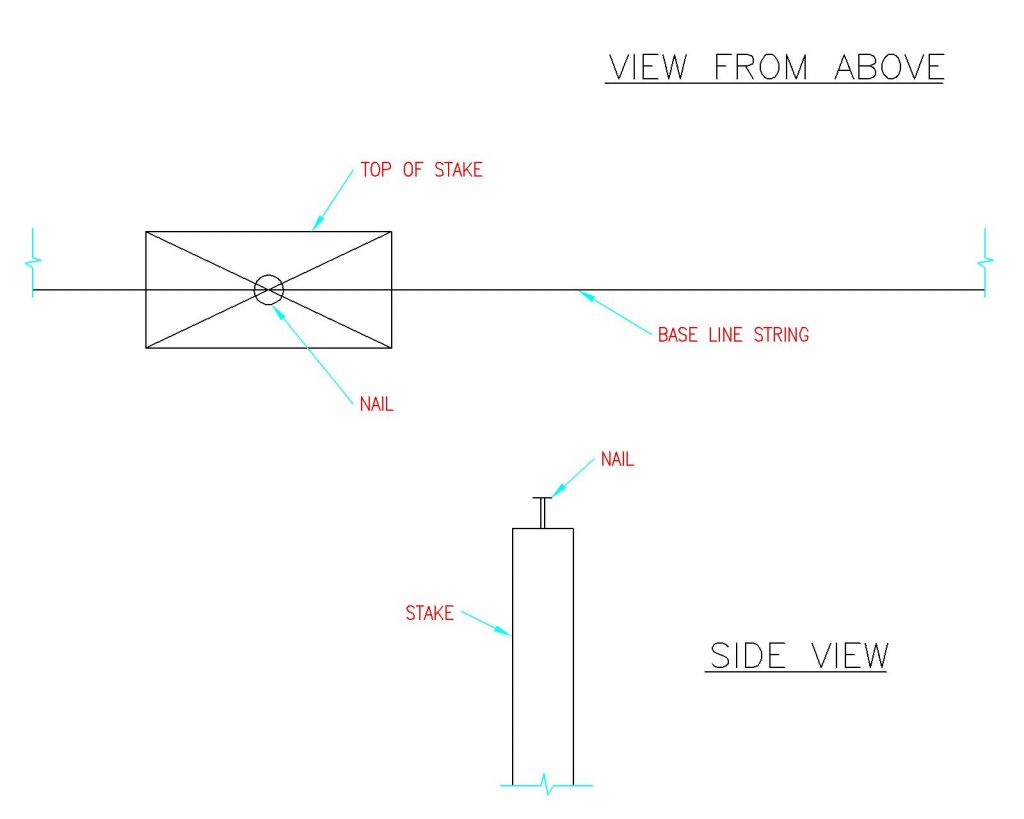
Figure 4-2: Placing Stakes
Hook a tape measure on nail at Stake A. Measure building length along base line from Stake A and set corner Stake B. See Figure 4-3
Use a construction level (transit) and drive Stake B in so Stake A and B tops are level. Drive a nail partially into Stake B top at exact building length (as measured from column outside to column outside).
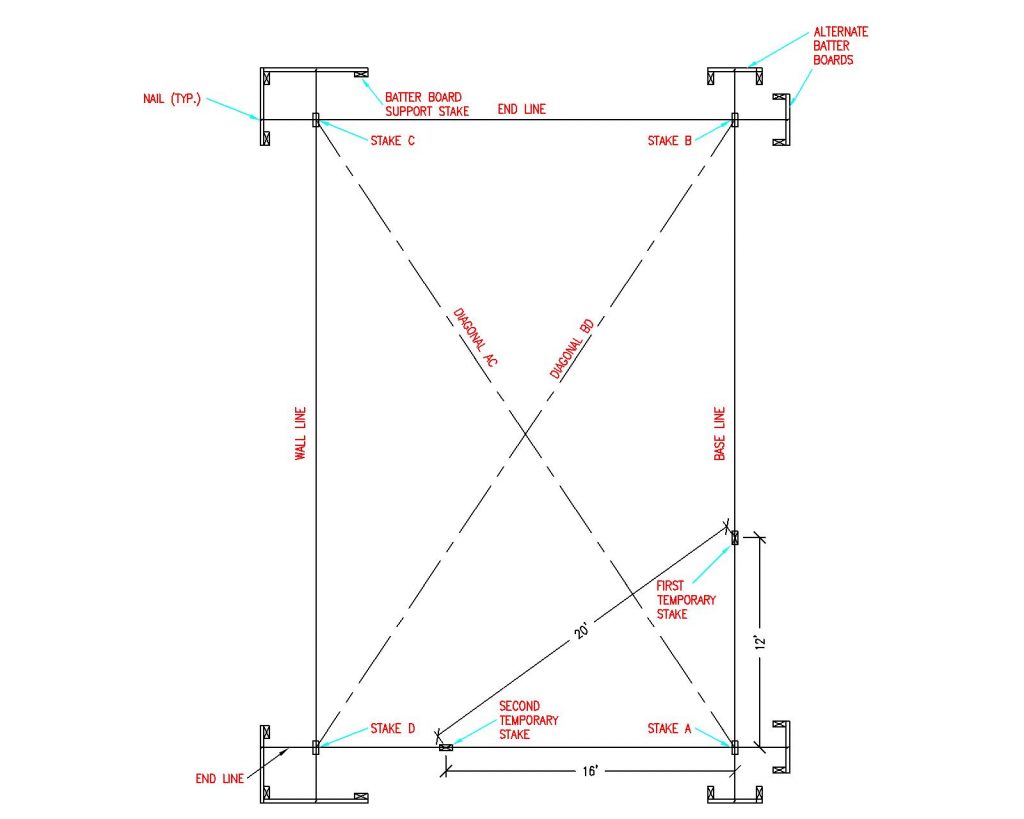
Figure 4-3: Batter Boards
Next make endwall perpendicular to sidewall. Measure 12 feet along the base line from Stake A and set a temporary stake. Intersection point 20 feet from this temporary stake and 16’ from Stake A is perpendicular to the base line. Set a second temporary stake at this point. (Figure 4-3)
Measure outside building width along this line and set Stake D. Drive Stake D into ground…level with Stake A and B tops. Drive a nail partially into Stake D top at exact outside building width. (Figure 4-3)
From nail in Stake D top, measure the outside building length. From nail in Stake B, measure outside building width. At two measurement intersection, drive last corner Stake C, with top level with previous three corner stake tops. As before, partially drive a nail into Stake C top, at exact outside corner point. (Figure 4-3)
Before proceeding, make certain all four corner stakes tops are level. Then double check, in this order – baseline length (A to B), Width B-C and A-D and then length C-D. Adjust nails or stakes B, C, or D as needed.
Diagonals AC and BD are to be equal for a rectangular building. Adjust by shifting C and D along the rear wall line.
Do NOT move A or B.
Keep widths B-C and A-D equal. Recheck any shifted stake levels.
Drive batter board stakes 8 to 12 feet from all corners. While specific batter board materials are not provided with building kit, girts make excellent batter boards, as long as they remain uncut and undamaged. Batter boards provide a level reference plane for building layout. Place to avoid interfering with excavation, pre-mix deliveries or construction and to remain undisturbed until columns are backfilled.
Level and fasten batter boards to stakes at same heights as corner stake tops.
Stretch building string lines between batter boards, barely touching nails on corner stake tops. Partially drive nails into batter board tops to line up string lines.
Temporary and corner stakes can now be removed. Corners will be located where lines cross.

Photo above shows corner column in hole with batter boards in place.
Mark Column Locations
Measuring along building lines, use small temporary stakes or nails painted with fluorescent paint to mark each column location center.

Remember to locate column center, ½ column thickness inside string lines. (Example: 5-1/2” column, column center is 2-3/4” inside string lines.) See Figure 4-4
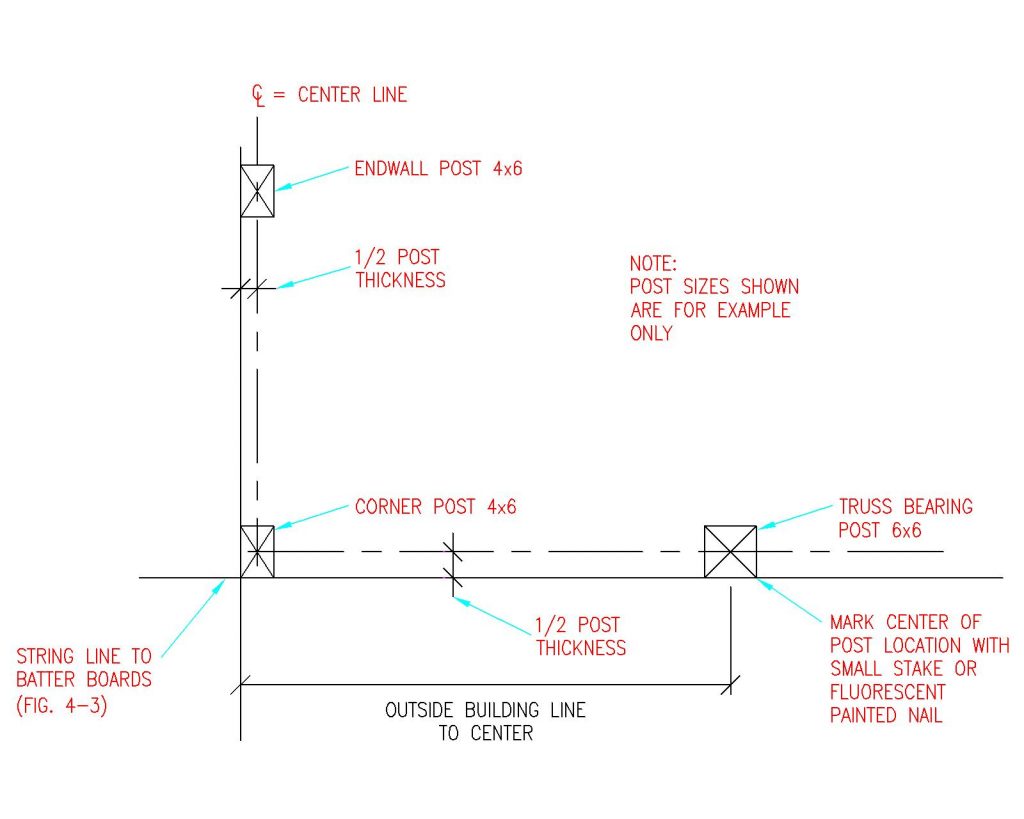
Figure 4-4: Offset String Lines
Figure 4-4 shows column centers as compared to “outside” building line.
After column centers have been located, offset (move) building line strings 1-1/2” (splash plank width), from column face outsides.
Why offset string lines? While this may sound confusing, failure to offset string lines could result in crooked finished walls, due to columns inadvertently touching lines. We’ve seen professional builders make this error far too often, and in this case, an ounce of prevention, is worth a pound of cure.
Once offset, building string lines will now measure 3” greater in dimension than building width and length (column outside to column outside).
Measure in from building string line 1-1/2 inches to set each column. Rather than having to use a tape measure each time, a 2×4 or 2×6 scrap block (happens to be 1-1/2” in thickness) can be placed between column and string line.