How Far Can a 2×6 Purlin Span?
Reader WILL in COMFORT writes:
“How far can a 2×6 purlin on a 6:12 sloped roof span?”
The following describes 2×6 SYP #2 purlins spanning a 14′ bay, with an on-center spacing of 24″ (sf).
Purlins are recessed between rafters with their top edges flush with rafter top edges. Purlins are mounted to rafters with Simpson Strong-Tie LU-26 joist hangers at both ends.
Effective simple beam span length (le) will be taken as 165.
Applied loads
Dead load, D[
Dpurlin: dead load from weight of purlin itself
Dpurlin = purlin density × ((b × d × le) / (sf × l))
Purlin density found via NDS Supplement 2015 Section 3.1.3:
density = 62.4 × (G / (1 + (G × 0.009 × moisture content))) × (1 + (moisture content / 100))
moisture content = 19%
density = 62.4 × (0.55 / (1 + (0.55 × 0.009 × 0.19))) × (1 + (0.19 / 100))
density = 34.56 pcf
Dpurlin = 34.56 pcf × ( ( 1.5″ × 5.5″ × 165″ ) / ( 24″ × 168″ ) ) × 1/12 in/ft
Dpurlin = 0.966 psf
Roof designed for 29g corrugated steel
Dead load from weight of steel (Dsteel) based on values from the American Building Components catalogue:
Dsteel = 0.63 psf
D: dead load
D = Dpurlin + Dsteel
D = 0.966 psf psf + 0.63 psf psf
D = 1.596 psf
Project load to a vector acting perpendicular to the roof plane:
D = D × cos(Θ)
D = 1.596 psf × cos(0.464)
D = 1.428 psf
A conversion from psf to psi will be made for ease of calculation:
D = 1.428 psf × 1/144 psi/psf
D = 0.01 psi
Roof live load, Lr
L: roof live load
Lr = 18 psf
Project load to a vector acting perpendicular to the roof plane:
Lr = Lr × cos(Θ) × cos(Θ)
Lr = 18 psf × cos(0.464) × cos(0.464)
Lr = 14.4 psf
A conversion from psf to psi will be made for ease of calculation:
Lr = 14.4 psf × 1/144 psi/psf
Lr = 0.1 psi
Snow load, S
S: snow load
S = 13.267 psf
Project load to a vector acting perpendicular to the roof plane:
S = S × cos(Θ) × cos(Θ)
S = 13.267 psf × cos(0.464) × cos(0.464)
S = 10.614 psf
A conversion from psf to psi will be made for ease of calculation:
S = 10.614 psf × 1/144 psi/psf
S = 0.074 psi
Wind load, W
W: wind load
W = 9.6 psf
A conversion from psf to psi will be made for ease of calculation:
W = 9.6 psf × 1/144 psi/psf
W = 0.067 psi
Wind uplift load, Wu
Wu: wind uplift load
Wu = -11.763 psf
A conversion from psf to psi will be made for ease of calculation:
Wu = -11.763 psf × 1/144 psi/psf
Wu = -0.082 psi
Lr ≥ S, so roof live loads will dictate in load combinations.
Bending test (fb / Fb′ ≤ 1.0)
Fb: allowable bending pressure
Fb′ = Fb × CD × CM × Ct × CL × CF × Cfu × Ci × Cr
CL = 1
CM = 1 because purlins are protected from moisture by roof
Ct = 1 NDS 2.3.3
CF = 1 NDS Supplement
Ci = 1 NDS 4.3.8
Cr = 1 NDS 4.3.9
S: section modulus
S = (b × d2) / 6
S = (1.5″ × (5.5″)2) / 6
S = 7.563 in3
w: pounds force exerted per linear inch of beam length
M: maximum moment
fb: maximum bending stress
Load combinations:
- D
CD = 0.9
Cfu = 1
Fb′ = 1000 psi × 0.9 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 900 psi
w = (D) × sf
w = 0.008 psi × 24″
w = 0.186 pli
M = (w × l2) / 8
M = ( 0.18559992381479 pli × (165″)2 ) / 8
M = 654.797 in-lbs
fb = M / S
fb = 654.797 in-lbs / 7.563 in3
fb = 86.585 psi
fb / Fb′ ≤ 1.0
86.585 psi / 900 psi ≤ 1.0
0.096 ≤ 1.0
- D + Lr
CD = 1.25
Cfu = 1
Fb′ = 1000 psi × 1.25 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1250 psi
w = (D + Lr) × sf
w = 0.108 psi × 24″
w = 2.586 pli
M = (w × l2) / 8
M = ( 2.5855999238148 pli × (165″)2 ) / 8
M = 9121.997 in-lbs
fb = M / S
fb = 9121.997 in-lbs / 7.563 in3
fb = 1206.214 psi
fb / Fb′ ≤ 1.0
1206.214 psi / 1250 psi ≤ 1.0
0.965 ≤ 1.0
- D + W
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + W) × sf
w = 0.074 psi × 24″
w = 1.786 pli
M = (w × l2) / 8
M = ( 1.7855999238148 pli × (165″)2 ) / 8
M = 6299.597 in-lbs
fb = M / S
fb = 6299.597 in-lbs / 7.563 in3
fb = 833.004 psi
fb / Fb′ ≤ 1.0
833.004 psi / 1600 psi ≤ 1.0
0.521 ≤ 1.0
- D + Wu
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + Wu) × sf
w = -0.074 psi × 24″
w = -1.775 pli
M = (w × l2) / 8
M = ( -1.7748379435325 pli × (165″)2 ) / 8
M = -6261.628 in-lbs
fb = M / S
fb = -6261.628 in-lbs / 7.563 in3
fb = -827.984 psi
fb / Fb′ ≤ 1.0
-827.984 psi / 1600 psi ≤ 1.0
-0.517 ≤ 1.0
- D + 0.75Lr + 0.75W
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + 0.75Lr + 0.75W) × sf
w = 0.133 psi × 24″
w = 3.186 pli
M = (w × l2) / 8
M = ( 3.1855999238148 pli × (165″)2 ) / 8
M = 11238.797 in-lbs
fb = M / S
fb = 11238.797 in-lbs / 7.563 in3
fb = 1486.122 psi
fb / Fb′ ≤ 1.0
1486.122 psi / 1600 psi ≤ 1.0
0.929 ≤ 1.0
- D + 0.75Lr + 0.75Wu
CD = 1.6
Cfu = 1
Fb′ = 1000 psi × 1.6 × 1 × 1 × 1 × 1 × 1 × 1 × 1
Fb′ = 1600 psi
w = (D + 0.75Lr + 0.75Wu) × sf
w = 0.021 psi × 24″
w = 0.515 pli
M = (w × l2) / 8
M = ( 0.51527152330431 pli × (165″)2 ) / 8
M = 1817.878 in-lbs
fb = M / S
fb = 1817.878 in-lbs / 7.563 in3
fb = 240.381 psi
fb / Fb′ ≤ 1.0
240.381 psi / 1600 psi ≤ 1.0
0.15 ≤ 1.0
Purlin stressed in bending to a maximum of 96.5%
Shear test (fv / Fv′ ≤ 1.0)
Fv: allowable shear pressure
Fv′ = Fv × CD × CM × Ct × Ci
CM = 1 because purlins are protected from moisture by roof
Ct = 1 NDS 2.3.3
Ci = 1 NDS 4.3.8
V: max shear force
fv: max shear stress
Load combinations:
- D
CD = 0.9
Fv‘ = 175 psi × 0.9 × 1 × 1 × 1
Fv‘ = 157.5 psi
V = w × (le – (2 × d)) / 2
V = 0.186 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 14.57 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 14.57 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 2.649 psi
fv / Fv′ ≤ 1.0
2.649 psi / 157.5 psi ≤ 1.0
0.017 ≤ 1.0
- D + Lr
CD = 1.25
Fv‘ = 175 psi × 1.25 × 1 × 1 × 1
Fv‘ = 218.75 psi
V = w × (le – (2 × d)) / 2
V = 2.586 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 202.97 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 202.97 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 36.904 psi
fv / Fv′ ≤ 1.0
36.904 psi / 218.75 psi ≤ 1.0
0.169 ≤ 1.0
- D + W
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = 1.786 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 140.17 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 140.17 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 25.485 psi
fv / Fv′ ≤ 1.0
25.485 psi / 280 psi ≤ 1.0
0.091 ≤ 1.0
- D + Wu
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = -1.775 pli × ( 165″ – (2 × 5.5″) ) / 2
V = -139.325 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × -139.325 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = -25.332 psi
fv / Fv′ ≤ 1.0
-25.332 psi / 280 psi ≤ 1.0
-0.09 ≤ 1.0
- D + 0.75Lr + 0.75W
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = 3.186 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 250.07 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 250.07 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 45.467 psi
fv / Fv′ ≤ 1.0
45.467 psi / 280 psi ≤ 1.0
0.162 ≤ 1.0
- D + 0.75Lr + 0.75Wu
CD = 1.6
Fv‘ = 175 psi × 1.6 × 1 × 1 × 1
Fv‘ = 280 psi
V = w × (le – (2 × d)) / 2
V = 0.515 pli × ( 165″ – (2 × 5.5″) ) / 2
V = 40.449 lbs
fv = (3 × V) / (2 × b × d)
fv = (3 × 40.449 lbs) / ( 2 × 1.5″ × 5.5″ )
fv = 7.354 psi
fv / Fv′ ≤ 1.0
7.354 psi / 280 psi ≤ 1.0
0.026 ≤ 1.0
Purlin stressed in shear to a maximum of 16.9%
Deflection test (Δmax / Δallow ≤ 1.0)
I: moment of inertia
I = b × d3 / 12 NDS 3.3.2
I = ( 1.5″ × (5.5″)3 ) / 12
I = 20.797 in4
E: modulus of elasticity
E′ = E × CD × CM × Ct × Ci
CM = 1 because purlins are protected from moisture by roof
Ct = 1 NDS 2.3.3
Ci = 1 NDS 4.3.8
Δallow: allowable deflection
Δmax: maximum deflection
Load combinations:
- D + Lr
CD = 1.25
E′ = 1400000 × 1.25 × 1 × 1 × 1
E′ = 1750000 psi
Per IBC 1604.3 footnote d, dead load may be taken as 0.5D.
w = ((0.5 × D) + Lr) × sf
w = ( (0.5 × 0.01 psi) + 0.1 psi ) × 24″
w = 0.104 pli
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 2.493 pli × (165″)4 ) / ( 384 × 1750000 psi × 20.797 in4 )
Δmax = 0.661″
Δmax / Δallow ≤ 1.0
0.661″ / 1.1″ ≤ 1.0
0.601 ≤ 1.0
- D + W
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 1.786 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = 0.37″
Δmax / Δallow ≤ 1.0
0.37″ / 1.1″ ≤ 1.0
0.336 ≤ 1.0
- D + Wu
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × -1.775 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = -0.368″
Δmax / Δallow ≤ 1.0
-0.368″ / 1.1″ ≤ 1.0
-0.334 ≤ 1.0
- D + 0.75Lr + 0.75W
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 3.186 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = 0.66″
Δmax / Δallow ≤ 1.0
0.66″ / 1.1″ ≤ 1.0
0.6 ≤ 1.0
- D + 0.75Lr + 0.75Wu
CD = 1.6
E′ = 1400000 × 1.6 × 1 × 1 × 1
E′ = 2240000 psi
Δallow = l / 150 IBC 1604.3
Δallow = 165″ / 150
Δallow = 1.1″
Δmax = (5 × w × l4) / (384 × E′ × I)
Δmax = ( 5 × 0.515 pli × (165″)4 ) / ( 384 × 2240000 psi × 20.797 in4 )
Δmax = 0.107″
Δmax / Δallow ≤ 1.0
0.107″ / 1.1″ ≤ 1.0
0.097 ≤ 1.0
Purlin stressed in deflection to a maximum of 60.1%
Some loads are expected to act on a structure for short time periods, such as wind and seismic loads whose duration would normally be measurable in seconds. Other loads, such as snow, might last at least three months, depending on geography. Dead loads are permanent and they are expected to act on a structure for its life. Load Duration Factors allow us to increase wood’s load carrying capacity based on how long a load is expected to act on a structure—shorter time period, higher allowed increase.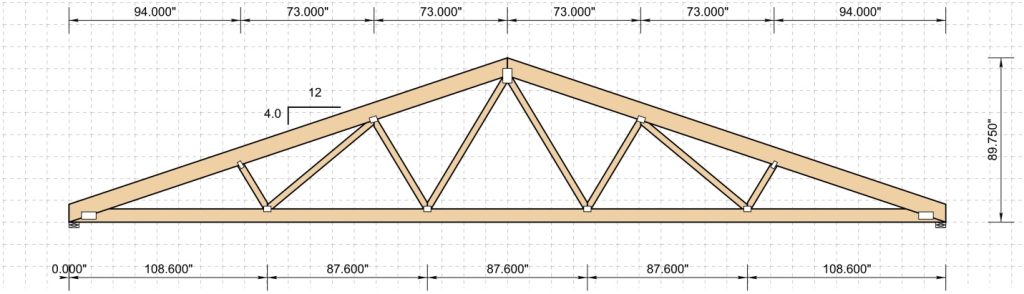
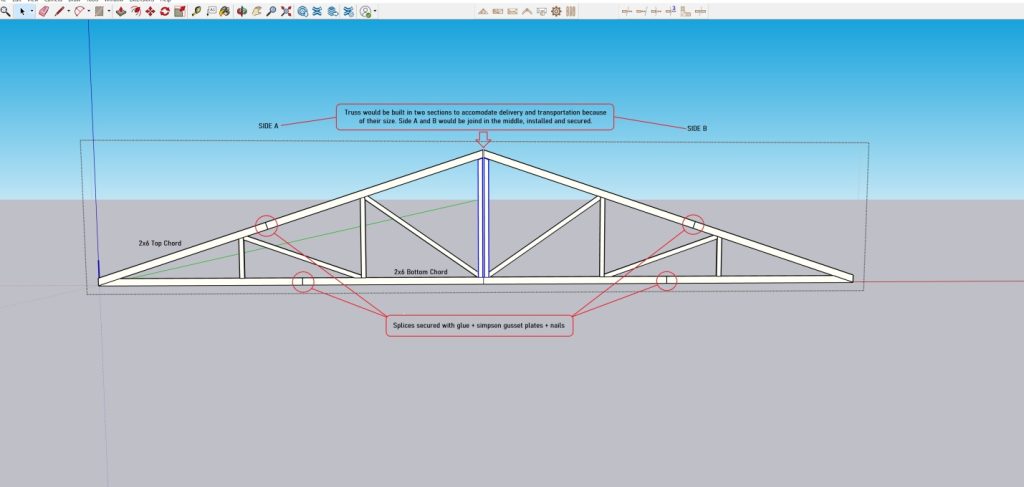
I spent two decades in management or owning prefabricated metal connector plated wood truss plants. In my humble opinion – attempting to fabricate your own trusses of this magnitude is a foolhardy endeavor, for a plethora of reasons:
Exposure determination is not relegated to a nice, comfortable chart or table. This section’s main part explains ground roughness variations from natural topography and vegetation need to be take into account when determining Exposure Category.
DEAR CHRIS: Closed cell spray foam is a great product, however it would not be my first choice for your climate zone. For best results, closed cell spray foam should be two inches or thicker to prevent condensation, and applied directly to the roof and wall steel. Hopefully you have a well-sealed vapor barrier beneath your building’s slab. With closed cell spray foam, you may experience condensation on your building’s interior, so do not be surprised should you have to mechanically dehumidify. Unless specified as necessary on your engineer sealed building plans, you should not add plywood or OSB to your roof system, as it will add unexpected dead loads to your building system.
DEAR POLE BARN GURU: Hello. We are wanting to build a 2 story pole barn winery. First floor winery and second would be air-bnb type rental. We aren’t sure if we should use attic truss or complete the build with a traditional second floor. Cost is probably biggest concern. Space second as we know attic truss would be less room. Would you do an attic truss or traditional 2nd floor type build and roughly cost difference between the 2? Building size will be roughly 40×60. Thank you for your time. CRAIG in ROCK CREEK
DEAR POLE BARN GURU: I built a pole barn for my r/v a couple of years ago. I used 4×4 for my posts with a metal roof and purlins with no siding. The posts are set 3′ into the soil with no concrete. Posts are 10′ out of the ground. When we get a strong wind the posts bend slightly at ground level allowing the structure to flex. Is there a way to add strength to the posts or do I need to replace with a larger size post and should I embed the post in concrete or will it rot? MARK in BRADENTON
As we see in Chapter 1 of the Post Frame Building Design Manual (PFBDM), post frame construction has been around for hundreds of years. The performance, life expectancy, and reduction of material and labor costs are all reasons that this type of construction is becoming more popular today. We see not only construction in agricultural settings, but residential construction is rapidly growing in today’s price and time conscious market. However, structural design is critical to ensure long life and adequate performance of the building. 
This is just one of many reasons why post frame buildings should be designed by a Registered Professional Engineer. 
Face it, we humans are dimensionally challenged. Even though we have an idea a basketball hoop will be at 10 feet, we think our car needs a door this height. We want to make certain you design a building with adequate spaces for your activities. This includes properly sized doors, properly spaced, to actually allow prized possessions in or out without damage to your building or something treasured.
BENEFIT
Concept of girts being nailed to column exteriors is they (in theory) do not have to be trimmed therefore saving labor (as well as any need to measure). Being ignored in this is lumber typically comes approximately 5/8 inch over specified lengths, making trimming needed anyhow. Most common column spacings are multiples of exactly two feet – eight, 10, 12, etc., and those 5/8 inches add up across a very long or wide post frame building.
Of course somewhere along the discussion between the Building Designer and the client this statement always seems to come up: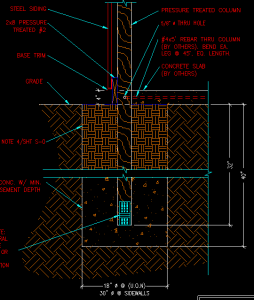
I was speaking to Rachel and she gave me your email to see if you might be able to answer a question for me. I hired complete a 50’x 80’ x 12’ pole barn here in Huntley, MT. The company showed up on the job yesterday and drilled the holes and started setting posts. Posts are 8’ center. They set the corner posts and maybe 6 sidewall posts and 4 endwall posts. The other posts were placed in the drilled holes and left for completion today/tomorrow. When I inspected the posts that were placed but not set (no backfill) I noticed that there was no footing or no cleats attached to post base to prevent uplift. When I questioned the owner of the company what he was using for footings he stated nothing added just solid tamped. I immediately called him and questioned his reasoning and got the I have been building these like this for 25 years. My question is on average what is the post load in psi on the 50’ x 80’ x 12’ pole barn with a 40# snow load? My soil has a bearing capacity of 2100 psi.”
